7 ベルヌーイ

　前回までで、分散機に必要な冷却熱量、冷水の温度、冷水流量の決め方を説明しました。モーターの定格容量の８０％、温度差２０℃、入口－出口の温度差５℃というだけのことです。

　ここまで決めることができても、実際に冷水を流せなければ意味がありません。実際にそんなことがけっこうあります。

　冷水が流れなくなる原因は、主に圧力損失と呼ばれる厄介者です。

　圧力損失が生まれる原因は色々とありますが、サラッピンの状態もしくは整備された状態として考えます（ゴミが詰まっているとかはないものとする）。

　圧力損失の説明をするためには、どうしてもベルヌーイの定理を避けては通れないので、私の解釈で概念だけ説明します。本来の説明は専門書なで勉強しましょう。

　と、その前に、３つの言葉を理解しておく必要があります。その言葉とは、層流と乱流とレイノルズ数です。この３つが概念として理解していないと、流体のことがほとんど説明できません。

　層流は整然とした流れのことをいい、乱流は不規則なながれのことをいいます。層流と乱流を区分けする指標がレイノルズ数です。なんやかんやと使う数字なので、覚えておいて損はありません。言葉だけ、流体といえば『レイノルズ数』。

　＜レイノルズ数＞

　　
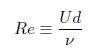
　　　円管の直径d，断面平均流速U，動粘性係数（絶対粘度を密度で割ったもの）ν

　レイノルズ数は無次元数といって、単位がありません。単位がないと単位を変換する必要がないし、どのような条件下でも同じように評価できるので非常に便利です。普通に生活していると、無次元数について考えることはありませんが便利な考え方です。

　層流は定常流と読み替えることができます。厳密にはちょっと違うのですが、大きくは間違っていません。つまり、『定常流という条件で成り立つ法則 (I)』は層流で成り立つ法則だということです。『渦なしの流れという条件で成り立つ法則 (II)』は『定常流という条件で成り立つ法則 (I)』をもうちょっと広い範囲で使えるようにしたものです。

　わかったような、わからんような感じですが、特に理解する必要はありません。

　ベルヌーイの定理というのは限定した条件で成り立つ定理で、人が普通に生活できるような場所で、水に限定すれば次の関係式が成り立つというものです。

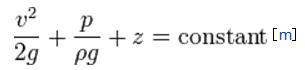
　速度水頭　＋　圧力水頭　＋　位置水頭　＝　一定

　運動エネルギー　＋　位置エネルギー　＝　一定

　ここで、いくつかポイントがあります。

　ベルヌーイの定理はエネルギー保存の法則からも導くことができます。エネルギー保存の法則では、運動エネルギーと位置エネルギーの和が一定という解釈になります。私はこの考え方の方がしっくりきます。

　もうひとつポイント。層流でしか成り立たないということです。なぜ、乱流だったら成立しないのでしょう？

　話を簡単にするために、先に圧力損失の計算方法について説明します。 　昔の人は偉かったですね。実際に流量をあれやこれや変えて実験をした人がいました。すると、なんかしらの損失があると気付いちゃいました。これが圧力損失です。圧力損失をベルヌーイの定理に当てはめると次のようになります。

　このhf（圧力損失）を無理矢理計算できるようにした式が次の式です。

　元々が実験式なので、理解しなくてもいいです。実験式を理論的に組み立てて、補正して、理屈で考えても納得できるような形にしてあります。圧力損失を計算する場合に必ず使用する式なので、使えるようにだけなりましょう。

　ムーディー線図？こいつが曲者です。 　横軸にレイノルズ数で縦軸にf（図ではλになっています）で、両軸とも対数の両対数グラフです。ε/dは配管の粗さを示す値です。

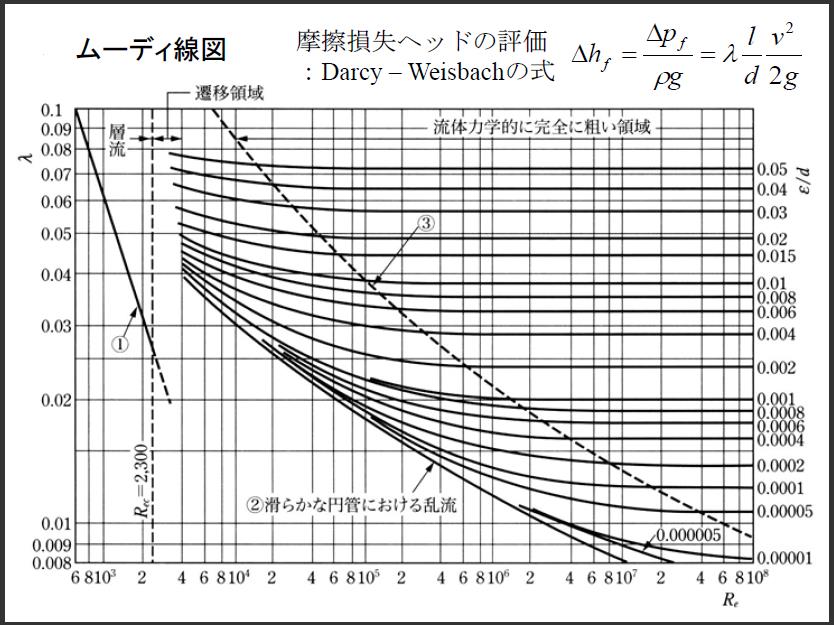
　これって、どないして読むねん？と、突っ込みたくなるグラフです。このグラフに頼らなくても計算できるので安心してください。

　層流域は直線、乱流域は曲線となっていることと、層流域では配管の粗さに関係ないことがポイントです。

　簡単に言うと、乱流域はややこしく、層流域は素直だということです。

　摩擦損失係数はレイノルズ数に依存する値で、レイノルズ数は流速に依存する値です。層流の場合、摩擦損失係数とレイノルズ数が比例関係にあるので、圧力損失は流速だけに依存するということになります。しかも、流速が遅いので、ほとんどの場合は実揚程だけを考慮すれば問題ありません。ベルヌーイの定理をそのまま適用しても問題ないくらいの誤差に収まります。ちなみに、50Aの配管で層流となるのは5L/min（Re≒2000）ぐらいの流量までです。 乱流の場合、摩擦損失係数はレイノルズ数が比例関係になく、配管の粗さにも影響されるので、ややこしいということになります。乱流の場合は、流速が大きなこともあって、流速の二乗に比例する圧力損失が大きくて無視できないわけです。ちなみに、50Aの配管であれば200L/minぐらいが目安なので、レイノルズ数は約80,000です。

　層流だと、流れが素直で、圧力損失が小さくて簡単に計算できるから、ベルヌーイの定理を使って説明できるけど、乱流だと流れがややこしくて説明しきれないということです。そうはいっても、乱流のときも計算できた方が便利なので、圧力損失を計算できるようにしたら、ベルヌーイの定理に合いましたとさ。ベルヌーイの定理に合わせようとしたら、こうやって圧力損失を計算すれば合うよ、でもＯＫ。

　現実の世界で、特に熱交換をするような場合は、層流ということは極めて稀で、むしろ如何にして乱流とするかを考えるぐらいなので、圧力損失を常に考慮する必要があります。そうしないと、ポンプの仕様も決まらないし、実際に流そうと思っても流せないなんてことになります。

　次は具体的に分散機の圧力損失を考えてみます。