撹拌機マスターへの道 5
前回は撹拌機の種類を整理しました。今回からは撹拌動力について整理を始めます。
様々な検討がされていて、立場によって入口が変わってくるのが撹拌動力の計算です。
立場の分岐点は、撹拌機を作る側か使う側の違いかと思います。
作る側の方は、論理的な裏付けが不可欠なので、先人たちの文献も参考にして基礎的な検討が必要かと思います。
私は使う側の立場なので、基礎的な検討は省きます。大昔にいくつか文献を読みましたが、ズバリ使えるものには出会えず、考え方だけを参考にさせていただきました。
私の理解は
- 〇〇の法則、〇〇の定理みたい式があるわけではなく、ニュートンの法則などに反しない特定条件での実験式しかない
- あらゆる形状に対応できるような都合の良いものはない
- 動力数Npとレイノルズ数Reがなければ始まらない
- 動力数Npとレイノルズ数Reは机上で求めるより、実験で求める方がはるかに簡単
- 撹拌機および容器の関係が相似形であればスケールが変わっても実験式は使える
ということです。
今時だと、撹拌装置をモデリングしてシミュレーションすることで実験式が求められるかもしれませんが、仮想で実験するか、実液で実験するかの違いなので本質は同じで、『やってみないとわからない』というのが私の印象です。たまたま先人が同じもの、近似しているものを検討していれば実験式を適用できるかもしれないので超ラッキー程度に考えた方が良いでしょう。
撹拌所要動力Pは動力数Np・液密度ρ・撹拌機の回転速度nの3乗・撹拌翼の径dの5乗に比例します。
【乱流域】P = Np ・ ρ ・ n3 ・ d5
【層流域】P = Np ・ Re ・ μ ・n2 ・ d3
P:動力 [W]、ρ :密度 [kg/m3]、n:回転数 [rps]、d:翼スパン[m]
動力数Npは撹拌翼の形状やレイノルズ数Reによって変化する値で、十分に流速があって乱流なら一定の値をとることが知られています。
レイノルズ数Reは次式で表され、無次元数です。無次元だからこそスケールに関係なく使えるので、この組み合わせを見つけたことが最大の発見かもしれません。
Re = ρ ・ n ・ d2 / μ
ρ :密度 [kg / m3]、n:回転数 [rps]、d:翼スパン[m]、μ:粘度 [Pa・s]
動力数Npとレイノルズ数Reの関係はグラフで表現されることが多いですが、層流域は両対数において比例関係なので近似式を求めるのは簡単です。遷移域で撹拌することは避けるべきことなので、無理やり近似する必要もないはずですが、データさえ読み取ればエクセルなどで近似曲線を求めるのは難しくないと思います。
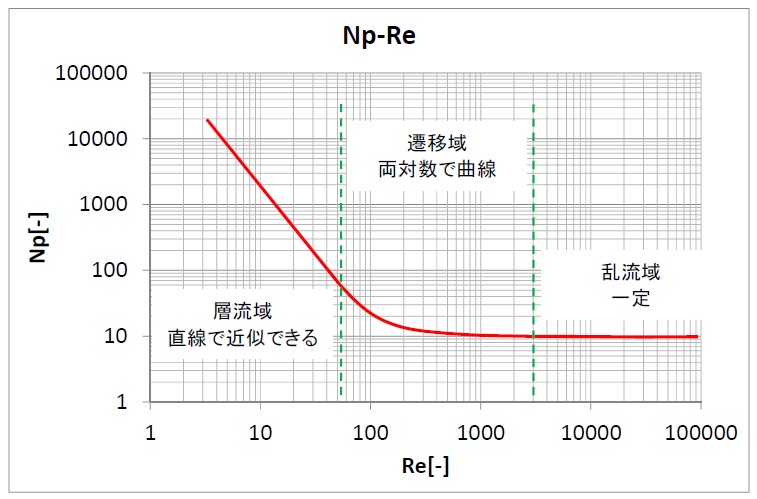
実験してNpとReの関係を導くことができさえすれば、撹拌所要動力を計算できることになります。
しかし、非ニュートン流体の場合はせん断によって粘度も変化することから、粘度一定とした前述の関係式がそのままでは使えなくなります。粘度変化の関係式を作るところから始めて、Np-Re線を作成したとしても層流域、乱流域が明確に現れるとは限らず、煩雑な計算になるはずです。おそらく手計算では無理かと思います。
非ニュートン流体を撹拌する場合の撹拌所要動力を求めるのであれば、実機での測定、もしくは相似形の実験機、もしくはシミュレーションとの併用で測定する方がはるかに楽だと思います。
次回は撹拌所要動力の測定について整理します。