5 対数平均温度差
分散機に必要な冷却熱量は計算できるようになりました。
モーターの定格容量 - 無負荷動力 = 必要な冷却能力
必要な熱量はわかったものの、具体的にどうやって冷やすか(熱を奪うか)が問題となります。分散機によっては、工水や上水を垂れ流しで冷やしているものもあります。垂れ流さないにしても、冷却装置に冷凍機ではなく冷却塔を使っている場合もあります。疑問に感じていない方もいるでしょう。どうやって冷やすかは重要なことで、大幅な省エネを達成できることもある考え方なので、分散機の冷却を例に掘り下げていきます。難しい説明は抜きにします。感覚で結果だけを身に付けましょう。
下図は熱交換の説明図でよく見かけるものです。
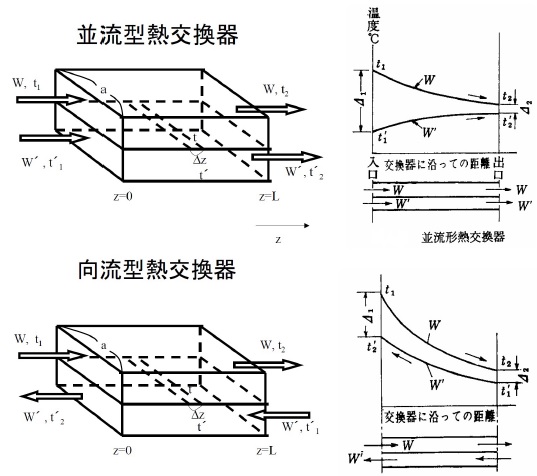
分散機もジャケット付のタンクも熱交換器に分散機能とか反応とかの機能が備わっていると考えてください。
感覚として、熱いものと冷たいものが熱交換器を介して接しているわけなので、熱が移動するのは理解できると思います。反応槽であれば、250℃以上ある熱媒をジャケットに流すことで、モノマーを150℃以上に加温したりします。分散機であれば、冷水をジャケットに流すことで、分散によって熱くなるミルベースを冷やしたりします。
何気に250℃以上の熱媒と書きましたが、反応槽内を250℃にするわけではないのに、なぜそれほどの高温が必要なのでしょうか?考えたことありますか?この感覚が重要なので、じっくり考えて自分のものにしていきましょう。
熱の透過率とか伝導率とか、乱流とか層流とかを考え始めると難易度が急激にあがるので、温度差に的を絞ります。細かいことを言い出せばキリがないのですが、熱交換をする部分(ジャケットの構造とか材質)はメーカーがちゃんと考えてくれているので、温度差だけを考えれば、実用上は問題ありません。
温度差について考えてきます。
なぜ温度差について考える必要があるのかというと、一般的に伝熱量は
伝熱量Q[W]=平均熱伝達率h[W/(m2・℃)]×伝熱面積A[m2]×対数平均温度差ΔT[℃]
で表現されるからです。平均伝達率と伝熱面積は設備が決まれば一定なので、対数平均温度差だけを考えれば伝熱量がわかっちゃうということです。
対数平均温度差
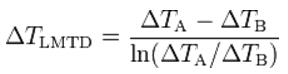
ただの温度差じゃなくって、『対数平均』って付いていますね。これには大きな意味があります。対数の平均です。ここポイントです。
温度差について考えるとして、何の温度を考えましょうか? 高温側も低温側も時々刻々と温度が変化していきます。さて、どこの温度差を考えれば良いと思いますか?入口?出口?真ん中ぐらい?いざ考えてみると答えが出てこないのでは?答えは簡単です。全部です。でも全部は計算できない(無限にあるから)ので、近似的に平均化して考えます。平均化するのは感覚として分かるような気がしませんか?近似的というのはどうでしょうか?
例えば分散機を考えた場合、分散機の中心部とべセル内壁近くだと温度が同じなわけありませんよね。たぶん、べセル内壁近くより中心部の方が温度は高いです。べセル内壁と中心部の真ん中は、平均温度になっていると思いますか?平均温度になっていれば、距離に対して直線的に変化しているということです。でも、そんなことはほとんどありません。
直線的に変化するのであれば、対数とする必要はありません。ただの平均温度差(直線近似)で十分です。直線的に変化しない場合は、何か別の手を考える必要があります。対数で近似すると結果が良く合います。厳密には温度分布が指数で近似されるので、式を変形させると対数となるわけです。詳しくは、下記を読んでみてください。
《対数平均温度差の導出》
対数平均温度を使わなければならないのは、熱交換器内部の流体の平均混合温度と壁面との温度差が、距離に対して直線的に変化していない場合です。流体同士の熱交換の場合は、その平均温度差が距離に対して直線的に変化していない場合です。
壁面温度一定の熱交換器の場合を考えます。
壁面温度をTw[℃]、流体の入口温度をT0[℃]、出口温度をT1[℃]とします。
式の導出はどのテキストにも出ているので、結果だけ書くと、熱交換器内部の流体の温度分布は
T(x) = Tw – (Tw – T0)*exp(-a*x/L) — (1)
となります(aは他の物理量を含む式ですが、xに依存しないので定数と考えます)。
熱交換器の長さをL[m]とすれば、出口温度がT1なので
T(L) = Tw – (Tw – T0)*exp(-a) = T1
となります。この結果から
a = log{(Tw -T0)/(Tw – T1)} — (2) → ここでlogが出現!
あるいは、
exp(-a) = (Tw -T1)/(Tw – T0) — (3)
となります。
壁面から流体への全熱流束Q[W]は
Q = ρ*cp*U/L*∫[x=0~L] [Tw – T(x)]dx — (4)
ρ:流体の密度[kg/m^3]、cp:流体の定圧比熱[J/kg/K]、U:流体の体積流量[m^3/s]
で表わされるので、式(1)を式(4)に代入して計算すれば
Q = ρ*cp*U/L*(Tw – T0)∫[x=0~L] exp(-a*x) dx = -m*cp* (Tw – T0)*[exp(-a) – 1]/a — (5)
式(2)と式(3)を式(5)に代入すれば
Q =ρ*cp*U*(T1 -T0) / log{(Tw -T0)/(Tw – T1)}
となって、全熱流束Q[W]は対数平均温度(T1 -T0) / log{(Tw -T0)/(Tw – T1)} 比例する。
熱交換器内部の流体の平均混合温度と壁面との温度差が、距離に対して直線的に変化しているとみなせる場合は
T(x) = T0 + (T1 – T0)*x/L と書けますので、同じ計算をすると、Q = ρ*cp*U*[Tw – (T0 + T1)/2] となって対数は出てきません。
ごちゃごちゃと説明をしていますが、要するに対数平均温度差が重要だということです。
対数平均温度差に比例して熱は移動するので、熱を加えたり、奪ったりする場合は対数平均温度差が大きい方が有利なのは感覚的に分かりますか?単に温度差が大きいというのとはちょっと違います。ここが感覚的に身に付いているかどうかの分かれ道です。
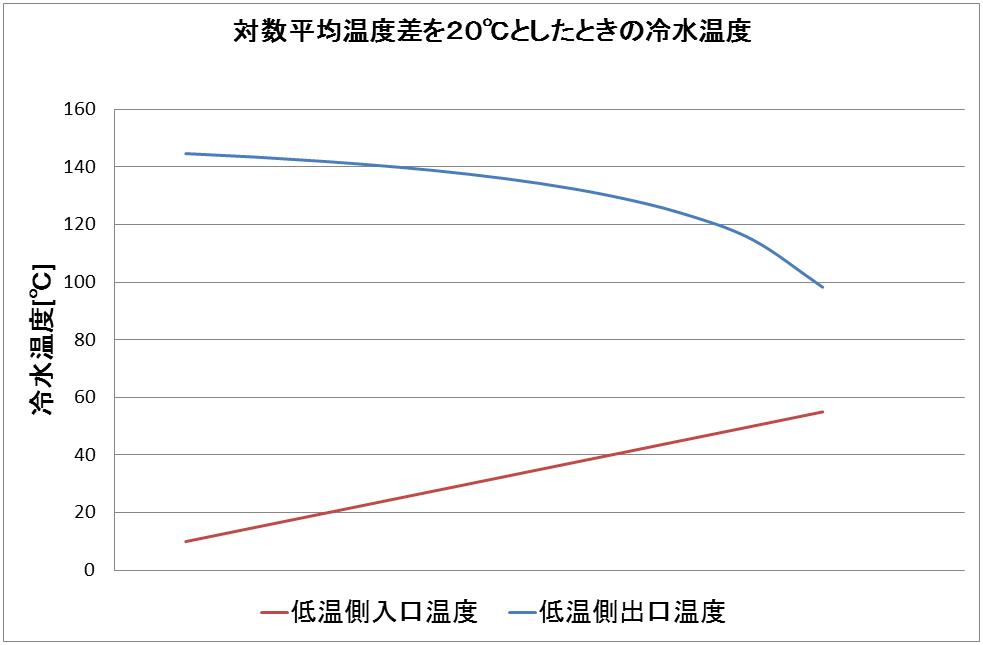
グラフを作ってみました。高温側の入口温度を150℃、出口温度を60℃とした場合に、対数平均温度差を20℃とするための低温側の入口、出口温度です。
冷水の入口温度が10℃で出口温度が140℃ぐらいと、入口温度が50℃で出口温度が125℃ぐらいだと対数平均温度差は同じなので、冷却能力は同じということになります。10℃の冷水は冷凍機が必要ですが、50℃なら冷却塔で十分ですよね。
もう一つグラフを作ってみました。
さっきのグラフでは、冷水の出口温度が140℃を超えています。現実にはありえませんよね。沸騰しちゃいますから。
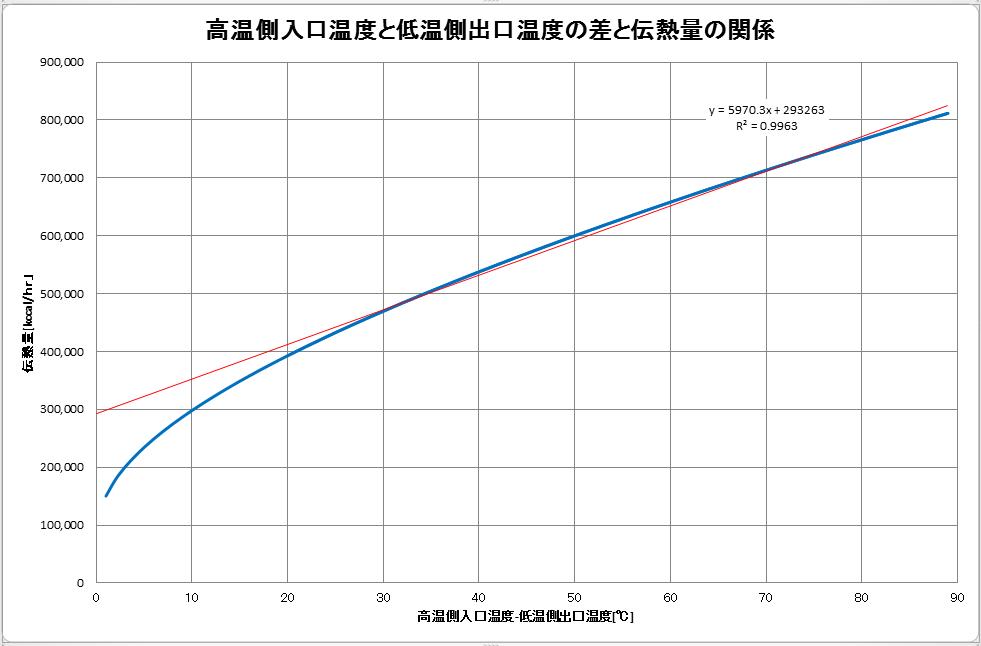
対数平均温度差が重要と説明しましたが、でも、それだけでは仕様を決めかねる場面に出くわすはずです。次のグラフをじっくり眺めてください。
20℃ぐらいで、直線近似曲線(赤線)から外れていることがわかると思います。これは、高温側と低温側の温度差が20℃未満になると熱伝達の効率が悪くなることを示しています。つまり、高温側と低温側の温度差が20℃以上確保できない場合は要注意です。
伝熱面積の大きさ次第ということになりますが、シェル&チューブ式(コンデンサーなど)とか、二重管式(分散機とかジャケット付タンクなど)は容積に対する伝熱面積が小さいので苦労します。プレート式熱交換器みたいに、容積に対して伝熱面積が大きい場合は高温側と低温側の温度差が小さくても熱交換が可能です。
やっと、本題に戻ります。
分散機を冷却する場合を考えましょう。
分散機のペースト出口温度は製品にもよりますが、40℃で管理したいなら、冷水温度は少なくとも20℃以下である必要があります。よって、20℃以下の冷水を冷却塔で作るのは難しいので冷凍機を使うことになります。
どうです?ピンときました? 次回は分散機の冷水流量について考えます。


