撹拌機マスターへの道 3
前回は粘度特性を整理しました。今回は速度分布について整理します。
撹拌とはつまるところ乱流を作ること。撹拌しても系内の速度分布がどうなっているか想像できていないと、混ざっていないところ(=乱流が発生していないところ)ができてしまいます。
せん断応力の関係式
せん断応力は粘性係数とせん断速度の積で表現されます。
ニュートン流体の場合はn=1なので粘性係数μ=粘度ηとなります。
nが1以外の場合は非ニュートン流体ということになります。
式1-1) η=μDn-1
式1-2) τ=μDn
η:みかけ粘度【Pa・s】
τ:せん断応力【Pa】
μ:粘性係数
D:せん断速度【s-1】
n:指数
nは横軸にせん断速度、縦軸にみかけ粘度としたグラフの形をせん断速度の累乗関数で近似したときの指数のことを指します。
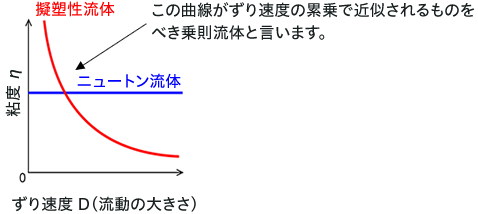
この関係が感覚的に理解できていないと、後々、混乱します。
速度分布
現象を簡単にするためにべき乗則流体の管内速度分布をみてみます。
べき乗則流体の管内速度分布は次式で表されます。
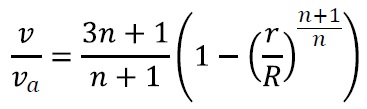
v=管内流速
va=管内平均流速
n=べき乗則流体の指数
R=円管半径
r=中心からの半径方向距離
内径50mmの配管を想定した速度分布は次の図となります。
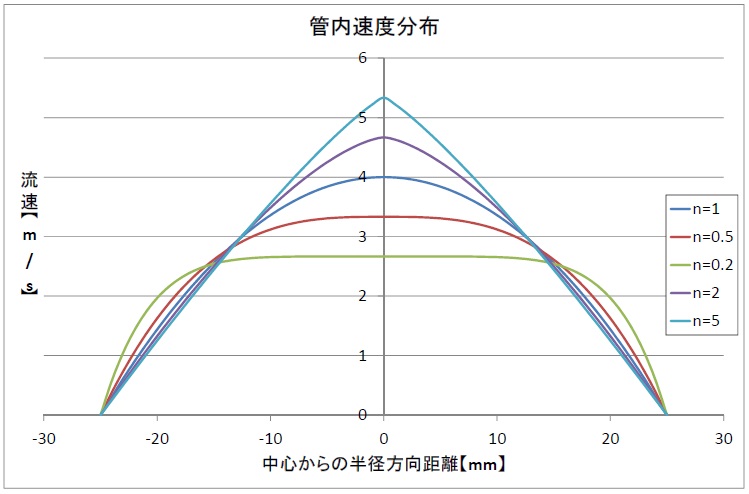
すべて平均流速は2m/sですが、nの違いで速度分布に大きな違いが生じていることがわかります。
次に、速度差を同様に表現してみます。速度差=せん断です。同じ速度で流れれば、相対的に位置が変化しないので混ざらない(撹拌されない)ということになります。
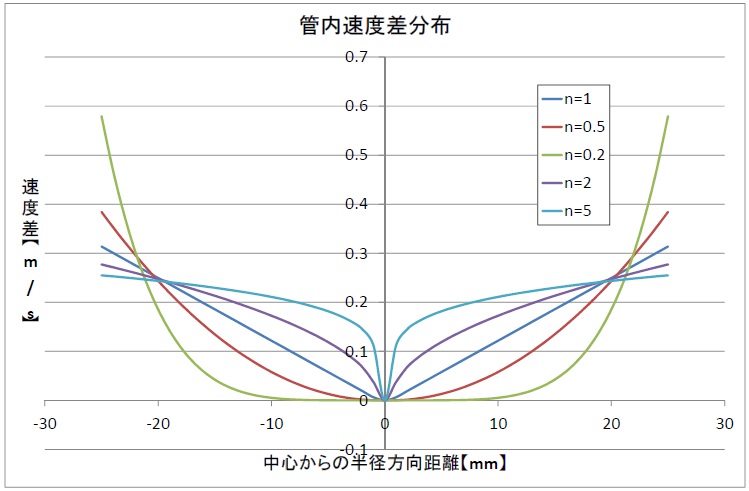
共通していえることは、管内壁面付近は速度差が大きい(速度勾配が大きい)のでせん断が働き、中心部は速度差が小さい(速度勾配が小さい)ので、せん断が働き難くなっています。
n値が大きい擬塑性流体やチクソトロピー流体は中心部付近で速度勾配が小さくなるので、せん断がかからず撹拌され難い。nが大きくなればなるほど、その範囲は広くなっています。逆にnが小さいダイラタンシー流体などは逆の傾向を示しています。
せん断がかかると粘度が下がる擬塑性流体やチクソトロピー流体の場合、管壁面付近は粘度が低く、中心部付近は粘度が高い状態なんだと思います。撹拌の操作に置き換えると、撹拌羽付近は粘度が低く、羽から離れるにしたがって粘度が上がる。いかに全体の速度勾配を大きくするかが必要になります。
せん断がかかると粘度があがるダイラタンシー流体の場合、管壁面付近は粘度が高く、中心部付近は粘度が低い状態なんだと思います。でも、粘度が低い領域は狭い。撹拌の操作に置き換えると、撹拌羽付近は速く動かせば動かすほど粘度が高くなって動いてくれず、撹拌羽に流体がまとわりつくように全体が流動する。ゆっくり、さっくり混ぜる操作が必要になります。
次回は撹拌翼の種類をみていきます。